Markov Functions
Markov State Probability Vector Function
Purpose
To represent a Markov State Probability Vector (SPV) and provide functionality for transitioning to a new SPV given a starting SPV and a Markov Probability Transition Matrix (TPM).
Type Name
‘markov_spv’
Definition Syntax
[spv_variable_key] : [markov_tpm_key]
where:
- ‘spv_variable_key’ is the key in the value dictionaryused that identify the starting or initial SPV at the start of the current period. See below on the syntax for defining a State Probability Vector (SPV).
- ‘markov_tpm_key’ is the key for the value dictionary that represents the Markov Transition Probability Matrix (TPM) to use when calculating the next State Probability Vector (SPV).
Syntax to Define a State Probability Vector
To define a SPV, use the following string syntax:
[prob_s1]|[prob_s2]|[prob_s3]|[prob_s1]
Where ‘prob_s1’, ‘prob_s2’ etc. are the probabilities associated with States 1,2, etc.
Thus, if the initial SPV looks like this:
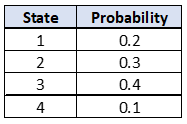
then to use this in a SPV JFunction, you need to code the SPV as follows:
‘0.2|0.3|0.4|0.1’
(you can leave spaces between numbers and pipe symbols if you want to).
Syntax to Define a Markov TPM
To define a Markov Transition Probability Matrix, use the following string syntax (shown here for a two-dimensional TPM):
[prob1_s1]|[prob1_s2] : [prob2_s1]|[prob2_s2]
This this is basically multiple SPV definitions separated by a colon (‘:’).
Thus, if the Markov TPM looks like this:
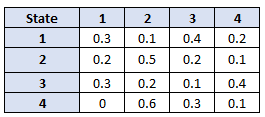
then to use this TM in a SPV JFunction, you need to code the TPM as follows:
‘“0.3|0.1|0.4|0.2 : 0.2|0.5|0.2|0.1 : 0.3|0.2|0.1|0.4 : 0|0.6|0.3|0.1’
(you can leave spaces between numbers and pipe symbols if you want to).
Code Once, use Often
At first glance, the above text-code for defining a Markov Transition Probability Matrix seems a bit complex and hard to read. However, this compact notation is needed so that you can easily code a model with multiple TPMs.
In your model, you will typically define a TPM as a Constant with the value being a text code as shown above. Thus you only have to code each TPM once, and then you can re-use it multiple times in your model.
The compact notation for defining a TPM means that you can pre-define multiple TPMs and assign to each one a key (e.g. ‘f_tpm_cracks_ac’). The TPM that applies to specific situations can then be easily be retrieved from the value dictionary at run time.
Since each TPM can be defined in a single line, having tens or even hundreds of TPMs in your model is not problematic. your model needs
Example
To illustrate the coding and use of a Markov State Probability Vector JFunction, we use the example given on Pages 6, 7 and 17 in the book by Sheskin (Sheskin 2011). This example assumes a weather model with the following states:
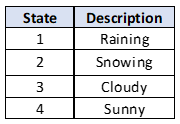
We assume that the Transition Probability Matrix for transitioning from one weather state to the next is as shown in Figure 2 above. For the example, we also assume the initial probabilities for the weather being in each of the defined states is as shown in Figure 1 above.
Now, using a Markov Chain process, we are interested to know what the probabilities are for being in each state at the end of the next period. The Markov Chain for this single step can be expressed in matrix form as follows:

Thus, if the probabilities for being in each state now is as shown in Figure 1, then the probability for being in State 2 after one period is 0.31.
To express this calculation in JFunctions, you need to first define the TPM as a constant using the syntax explained above. We assume the initial SPV is held in a model parameter with code ‘par_weather_spv’. This will be a text parameter and the value will be a code as shown above for SPV definition.
Thus our JFunction Block to define this Markov model will look like this:

Remembering that JFunctions execute from top to bottom, let us see how Juno Cassandra will use this JFunction block:
- The Markov TPM is defined as a Constant in the first row of the definition table and assigned to key ‘f_weather_tpm’ in the value dictionary.
- The Initial SPV is also defined as a Constant in the second row of the definition table and assigned to key ‘f_weather_initial’ in the value dictionary.
- When the JFunction block is executed at runtime, the value for key ‘f_weather_initial’ will be assigned to key ‘par_weather’ when line 2 (row 3 in the table) is executed.
- In line 3 (row 4 in the table), we define the SPV JFunction by specifying
- which key provides the initial SPV (‘par_weather’ in this case); and (b) by specifying the key that maps to the TPM code. We assign this JFunction to the key ‘f_weather_spv’
- When this JFunction SPV executes, the resulting value will be a string with value ‘0.24|0.31|0.21|0.24’ mapping to the right side of Figure 4 above. This value will also be assigned to key ‘par_weather’, thereby updating the value for ‘par_weather’ at the end of the period.
In the above example, we assumed that the initial weather state was already expressed as a SPV (held against key ‘f_weather_initial’). In a real modelling situation, you will typically have a known initial STATE rather than probabilities associated with each state.
This means you have to convert the known initial state to a SPV before you can use it in a Markov Chain. As shown in the following section, the State-to-SPV JFunction facilitate this transform from a known state to a coded SPV that is ready to use in a JCass Markov model.
Similarly, the SPV-to-State JFunction makes it easy for you to extract the expected state from the SPV at any stage. For example, if you want to express the most likely state at a given epoch, then you can use the SPV-to-State JFunction to collapse the SPV to a fixed state value.
Markov State-to-SPV Function
Purpose
To convert a known initial Markov state (e.g. ‘3’) to a state probability vector (e.g. [0,0,1,0]) in an encoded format (e.g. ‘0|0|3|0’) so that the coded SPV can be used to calculate a Markov chain using Markov SPV Function.
Type Name
‘markov_state_to_spv’
Definition Syntax
[param_key] : [number_of_states]
where:
- ‘param_key’ is the key in the value dictionary mapping to the parameter that holds the State to convert to a SPV, assuming 1-based index of the state.
- ‘number_of_states’ is the number of states to assume.
Comments
To start a Markov Chain calculation, your Markov variable will typically be in a known state. That is, you will know with certainty what state the variable is in initially. The state is known because you will typically start with an observed state.
The SPV is a probability vector, and thus the probability associated with the known initial state will be 1.0, whereas the probability for all other states is zero initially.
To use the known initial state in a Markov Chain, we have to convert the state to a SPV. For example, if we have a 5-state model and the known initial state is 2, then the associated SPV will be [0,1,0,0,0]. Or in coded form for use in JFunctions, the SPV will be ‘0|1|0|0|0’. Note that the vector holds 5 values which maps to a 5-state model.
The State-to-SPV JFunction makes it easy to convert an initial state to a coded SPV value.
Example
Assume we have a Markov variable held by the key ‘par_pci’ and that the variable has 4 states. We know that on a specific element the current state is 3. Then the coded version of the associated SPV should be: ‘0|0|1|0’.
To code this as a State-to-SPV JFunction, our setup code should look like this:
‘par_pci : 4’
This colon-delimited string code tells Juno Cassandra that the state value is mapped to key ‘par_pci’ in the value dictionary. The ‘4’ tells Juno Cassandra that there are 4 states.
Thus, if the value mapping to key ‘par_pci’ is 2, the resulting SPV code will be ‘0|1|0|0’.
Markov SPV-to-State Function
Purpose
To convert a coded representation of a State Probability Vector (SPV) to a definite State value (e.g. ‘2’). This function is the inverse of the State-to-SPV JFunction.
Type Name
‘markov_spv_to_state’
Definition Syntax
[spv_key] : [collapse_method]
where:
- ‘spv_key’ is the key in the value dictionary mapping to the coded SPV value (e.g. ‘0.1|0.3|0.5|0.2|0’) from which the state should be extracted/estimated.
- ‘collapse_method’ is method used to collapse the Expected Value to a State value (see comments below).
Collapse Methods
To convert a State Probability Vector to a State, we always first calculated the expected value by taking the dot-product of the SPV and the assocated states. Thus, if the SPV in coded format is: ‘0.24|0.31|0.21|0.24’, then this means there are 4 states, and the 1-based State Vector is therefore ‘1,2,3,4’. The expected value is thus the dot-product, or weighted sum, of these two vectors. You can verify for yourself that for this example, the expected value is 2.45.
We now have several options in how we want to convert this value of 2.45 to a definite state such as 1,2,3 or 4. The option you want to use needs to be specified by the ‘collapse_method’ parameter in the setup code.
Valid collapse method names are:
- ‘none’ : in this case the expected value is reported ‘as-is’ which means that the state will be represented by a real number.
- ‘floor’ : in this case the Floor() function is used to convert the expected value to the largest integer less than or equal to the expected value. Thus if the expected value is 2.44, the state that is returned will be 2.
- ‘ceiling’ : in this case the Ceiling() function is used to convert the expected value to the largest integer greater than or equal to the expected value. Thus if the expected value is 2.44, the state that is returned will be 3.
- ‘round’ : in this case the expected value is rounded to zero decimals. Thus if the expected value is 2.44, the state that is returned will be 2.
Comments
A Markov SPV JFunction allows you to take a coded string that represents the current, or starting SPV in the current epoch and then use a specific Markov TPM to calculate the SPV at the next epoch.
Note that the variables matching the keys provided for ‘spv_variable_key’ and ‘markov_tpm_key’ should be strings that contain the codes that defines the current SPV and the Markov TPM, respectively. The syntax for these codes is explained below.
The result from this function is a coded string that represents a SPV and can in turn be used as a SPV in further calculations. The example below clarifies these concepts.
It should be noted that by definition the probabilities in a State Probability Vector should always add up to 1.0. Similarly, the row vectors in a Transition Probability Matrix (TPM) should also add up to 1.0.
It is your job as a modeller to ensure that your Markov TPMs adhere to these definitions. Because of the repetitive nature of incremental models, and for performance reasons, Juno Cassandra will not do these check for you at runtime. So please be careful when coding up your Markov TPMs. It is also recommended that you do test calculations to ensure that the SPVs that are returned from Markov Chains always add up to 1.
Note that Juno Cassandra will round probabilities to 4 decimals when it converts a SPV to a coded string format. This may lead to small discrepancies between your calculations and those shown by Juno Cassandra outputs.